算法

Master 定理

\(O\)：表示上界（tightness unknown），即小于等于

\(\Theta\)：该时间复杂度既是上界也是下界（tight），即等于的意思

\(\Omega\)：表示下界（tightness unknown），即大于等于的意思

递推公式的复杂度计算，n 是问题规模，b 是递归子问题的数量，n/c 为每个子问题的规模（假设每个子问题的规模基本一样），f(n) 为递归以外进行的计算工作。

\(T(n)=b*T(\frac{n}{c})+f(n)\)

如果对任意正数 \(\epsilon \(，\)E = lg(b) / lg(c) = lg_c{b}\)

\(f(n) = O(n^{(E−\epsilon)})，则T(n) = \Theta(n^E)\)；
\(f(n)= \Theta(n^E)，则T(n)=Θ(f(n)log⁡(n))\)；
\(f(n)=Ω(n^{(E−ϵ)}), 且对某个δ≥ϵ有f(n)=Ο(n^{(E+δ))}，则T(n)=Θ(f(n))\)；

示例：

二叉树遍历：\(T(n)=2*T(\frac{n}{2}) + \Omega(1)=\Theta(n)\)
归并排序：\(T(n)=2T(\frac{n}{2}) + \Omega(n)=\Theta(nlog n)\)

递归转循环

代码实现见 Java数据结构与算法的递归部分。

递归转循环的通用方法：通过手动模拟栈帧的执行。

// 树的后序遍历：递归版
public static <E> void postOrderRecursive(BinaryTreeNode<E> root, List<E> store) {
    if (root == null) {
        return;
    }
    if (root.getLeft() != null) postOrderRecursive(root.getLeft(), store);
    if (root.getRight() != null) postOrderRecursive(root.getRight(), store);
    store.add(root.getVal());
}

// 树的后序遍历：非递归版
public static <E> void postOrder(BinaryTreeNode<E> root, List<E> store) {
    if (root == null) {
        return;
    }
    Deque<Frame<E>> stack = new LinkedList<>();
    stack.add(new Frame<>(root, store));
    while (!stack.isEmpty()) {
        Frame<E> current = stack.getLast();
        switch (current.pc) {
            case 0:
                if (current.node == null) stack.removeLast();
                break;
            case 1:
                if (current.node.getLeft() != null) stack.add(new Frame<>(current.node.getLeft(), store));
                break;
            case 2:
                if (current.node.getRight() != null) stack.add(new Frame<>(current.node.getRight(), store));
                break;
            case 3:
                store.add(current.node.getVal());
                break;
            case 4:
                stack.removeLast();
                break;
        }
        current.pc += 1;
    }
}
// 栈帧保存的内容
private static class Frame<E> {
    int pc;
    BinaryTreeNode<E> node;
    List<E> store;
    public Frame(BinaryTreeNode<E> node, List<E> store) {
        this.pc = 0;
        this.node = node;
        this.store = store;
    }
}

极大极小算法

极小极大实际上使用了DFS来遍历当前局势以后所有可能的结果，通过『最大化』自己和『最小化』对手的方法获取下一步的动作。

需要一个局面评估器，评估当前步骤的得分，启发式算法；
α-β剪枝也是类似的思想，只不过效率更高，因为它删减了一些不需要遍历的结点。

数学

四平方和三平方定理

四平方定理：任意自然数都可以表示成四个整型的平方和；
三平方定理：形式不为4^n * ( 8 * k + 7)的自然数可以表示成三个整型的平方和；

洗牌算法（Fisher-Yates shuffle）

概率均等

选出第一张和任意一个1到n的牌换；选出第二张和任意2-n的牌换；依次直到n-1选出n-1到n的牌换；共n-1次交换；

// To shuffle an array a of n elements (indices 0..n-1):
for i from n−1 downto 1 do
     j ← random integer such that 0 ≤ j ≤ i
     exchange a[j] and a[i]

// To shuffle an array a of n elements (indices 0..n-1):
for i from 0 to n−2 do
     j ← random integer such that i ≤ j ≤ n-1
     exchange a[i] and a[j]

完美洗牌算法

参考文献：A Simple In-Place Algorithm for In-Shuffle

有个长度为2n的数组{a1,a2,a3,…,an,b1,b2,b3,…,bn}，希望排序后{b1, a1, b2, a2,…., bn, an}，时间复杂度O(n)，空间复杂度O(1)的解法。

以 n = 4 为例，看到下标的变化：原下标 i => 新下标 ( 2 * i ) % ( 2 * n + 1)

序号	1	2	3	4	5	6	7	8
原数组	a1	a2	a3	a4	b1	b2	b3	b4
排序后数组	b1	a1	b2	a2	b3	a3	b4	a4

可以看出两个循环，每个循环可以O(1)时间替换；

1 -> 2 -> 4 -> 8 -> 7 -> 5 -> 1
3 -> 6 -> 3

如何寻找每个循环的开始：

对于 2 * n =（3^k-1）这种长度的数组，恰好只有k个环，且每个环的起始位置分别是 1, 3, 9，…3^(k-1) 。
如果 2 * n 不是 3^k-1 的倍数，总可以找到最大的整数m，使得m< n，并且2 * m=（3^k-1）；
前2m个元素：将m 到m+n的数组循环左移n-m次（通过三次数组反转实现）；
- 前2m个元素需要分别为a1,a2...am,b1,b2...bm

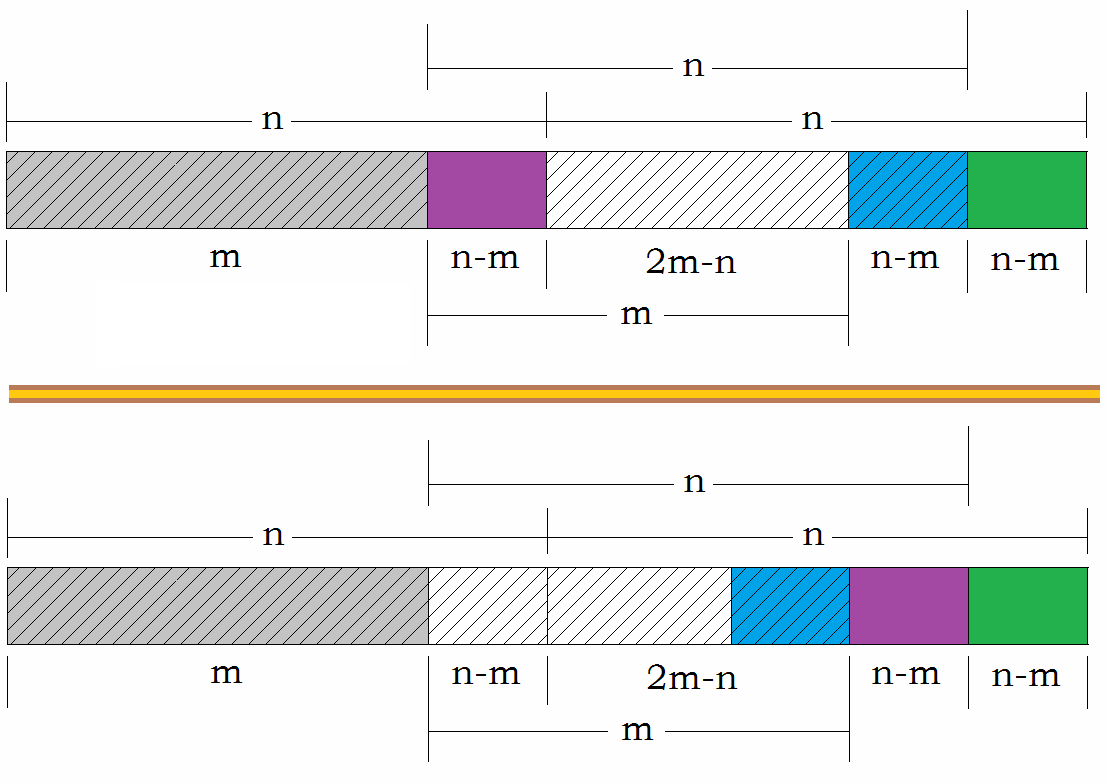
三次反转示例

2 * (n-m) 的规模可以通过循环替代得到，n = n - m，继续处理，至 n <1