跳转至

M2: 并行 Longest Common Subsequence (plcs)

M2: 并行 Longest Common Subsequence (plcs) (jyywiki.cn)

1. 背景

“最长公共子序列” (Longest Common Subsequence, LCS) 是大家熟悉的算法问题，问题的定义如下：

给定两个字符串 A 和 B，现在允许从 A 和 B 中分别删除任意数量的字符，但字符的出现的顺序不能改变，得到字符串′A′ 和 ′B′。问如何删除，使得：

  • C=A′=B′，即删除剩下的字符串相同，C 被称为A 和 B 的一个 “公共子序列”；
  • ∣C∣ 即公共子序列的长度最大。

以下是一些例子：

  • LCS("abcde", "ace") = 3, LCS 为 ace
  • LCS("bcdaacd", "acdbac") = 4, LCS 为 cdac
  • LCS("abc", "def") = 0

LCS 是一个十分经典的算法问题，也是 “动态规划” 算法的典型代表。大家可以在互联网上查找 LCS 问题的求解方法；或是在互联网上寻找讲解最长公共子序列的视频教程。

2. 实验描述

在这个实验中，我们已经提供了一个单线程的 LCS 算法实现。你需要将它并行化，使它能利用多处理器并行的计算力加速计算。

注意：存在一些算法 trick 能加速 LCS 的计算，但我们的要求是将我们给出的 naive 动态规划算法并行化。

2.1 总览

​ \(plcs [T]\)

2.2. 描述

创建 T (T≤16) 个线程求解字符串的最长公共子序列。plcs 命令从标准输入中读取两个字符串，并将 LCS 的长度输出到标准输出。我们保证输入字符串的长度均不超过 10,000。

当不提供参数 T 时，T=1，即串行求解。

2.3. 解释

框架代码中已经包含了串行 LCS 的实现，它的功能是正确的 (创建了多个线程，但不能并行求解)。你在并行化的过程中，需要遵守以下约定：

  • 你不能创建超过 T 个线程 (main 所在的线程不计入，因此你可以利用 main 线程)
  • 你只能使用纯粹的计算和给出的框架代码 thread.h/thread-sync.h 中提供的 API (其中包括 lock 和 unlock)

请特别注意：lock/unlock 只能保护和其他 lock/unlock 代码之间的互斥；持有锁的线程仍然会和其他不使用 lock/unlock 的代码在多个处理器上并行执行。此时，访问共享内存 (至少有一个是写) 将导致数据竞争，这是一种很常见的并发 bug。

3. 正确性标准

首先，你的程序仍然应该能够正确输出最长公共子串 LCS 的数值。

其次，你不应该大幅修改我们给出的算法，因此，我们预期在 T=1 时，你的代码的运行时间与框架代码相当。

在此基础上，我们需要观测到在字符串的长度足够大 (如 10,000) 时，你的代码在一个多处理器 (不少于 4 个处理器) 的 Online Judge 评测机上，T=1,2,4 时接近于 T 倍的线性加速。

4. 实验指南

4.1. 寻找并行的机会

我们可以把 LCS 的动态规划算法 (无论是递归求解，还是迭代求解) 都看成是一个有向无环图上的计算：为了得到f(i,j) 的值，我们就需要f(i−1,j)、f(i,j−1) 和 f(i−1,j−1) 的值。只有在这三个值都被正确计算的前提下，我们才能正确计算 f(i,j)：

img

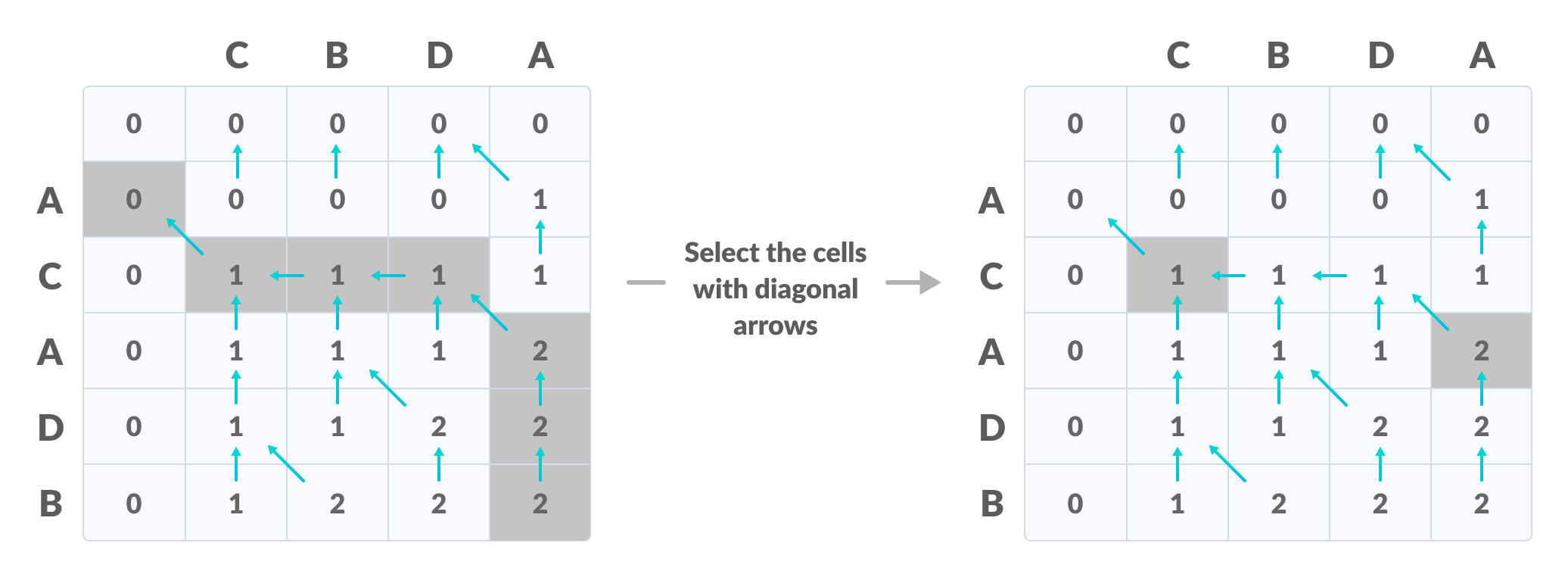
很自然地，我们选择用任何 “计算图” 上的拓扑序计算，就可以保证每个节点计算时，它需要的数据都已经准备好，于是有了框架代码中的二重循环，它代表了一种拓扑顺序：

for (int i = 0; i < N; i++) {
  for (int j = 0; j < M; j++) {
    // Always try to make DP code more readable
    int skip_a = DP(i - 1, j);
    int skip_b = DP(i, j - 1);
    int take_both = DP(i - 1, j - 1) + (A[i] == B[j]);
    dp[i][j] = MAX3(skip_a, skip_b, take_both);
  }
}

然而，里层循环却不能被直接并行：当 i 固定时，计算 f(i,j) 需要 f(i,j−1) 的值。那么，应该按照什么样的顺序计算呢？不妨把矩形旋转 45 度——你会发现，我们可以在 2n−1 “步” 之内计算完所有节点上的数值，而每一步里的节点都是可以并行计算的：

img

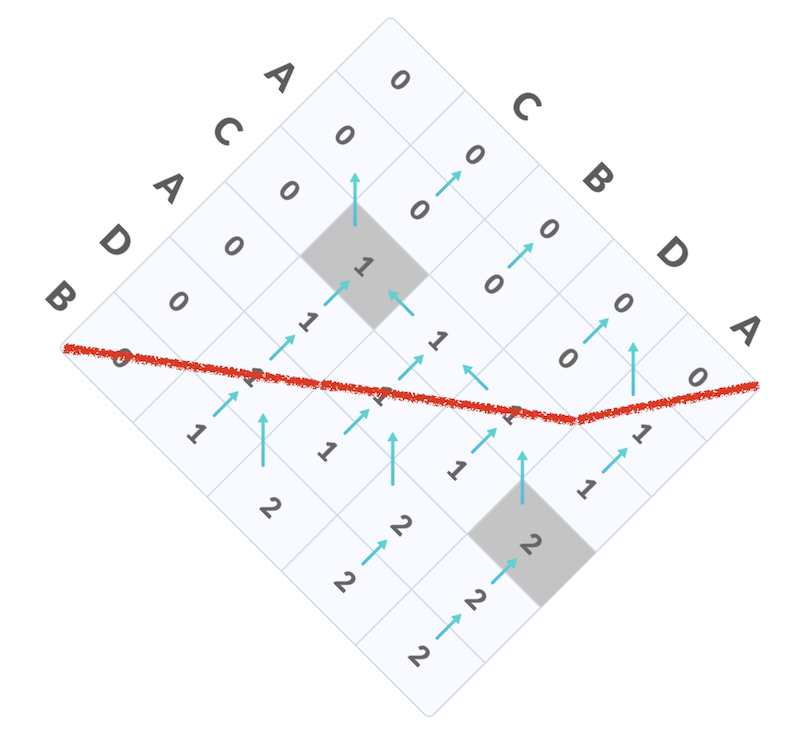
在这张图中，只要红线 “上面” 的 f(i,j) 都被正确计算出来，红线上的 f(i,j) 就可以并行计算。当字符串长度足够时，每个线程就可以分配到足够的工作量了。

4.2. 并行算法设计原理

如果我们把每个节点看作是消耗时长大致相等的计算、把边看成是节点计算的依赖关系，我们就得到了计算的依赖图 (dependency graph)。计算图的深度决定了并行算法的时间下限——任何一条长度为 d 的路径都意味着我们需要至少 d 步的串行计算。而在每个节点的计算时间远远大于线程调度/同步开销时，假设\(T_n\) 是 n个处理器执行的最优时间，那么有 Brent's Theorem

​ \(\frac{T_1}{p} \le T_p \le \frac{T_1}{p} + T_{\infty}\)

由于 \(T_{\infty}\) 则可以通过在计算依赖图上立即并行执行一切可执行的计算实现，这个结论意味着我们几乎总是可以并行 “可并行” 的部分。在实际并行化程序时，我们可以把计算图分成若干轮次的迭代 (例如 LCS 中，根据对角线划分迭代的轮次)，在每一个轮次中，均匀地把任务分配给各个线程执行。

4.3. 实现并行求解

在理解了并行算法的设计原理以后，实现并行 LCS 就不困难了：

for (int round = 0; round < 2 * n - 1; round++) {
  // 1. 计算出本轮能够计算的单元格
  // 2. 将任务分配给线程执行
  // 3. 等待线程执行完毕
}

上面的代码框架可以使用同步，也可以使用互斥实现。另外值得一提的是，当本轮计算量足够小时，并行化带来的收益未必划算 (执行额外同步操作的时间可能和直接串行执行相差无几)。此外，缓存访问的局部性也是并行化算法的一个重要考虑。这部分内容交给大家自由探索。