数组

所有代码实现见 Java数据结构与算法

堆

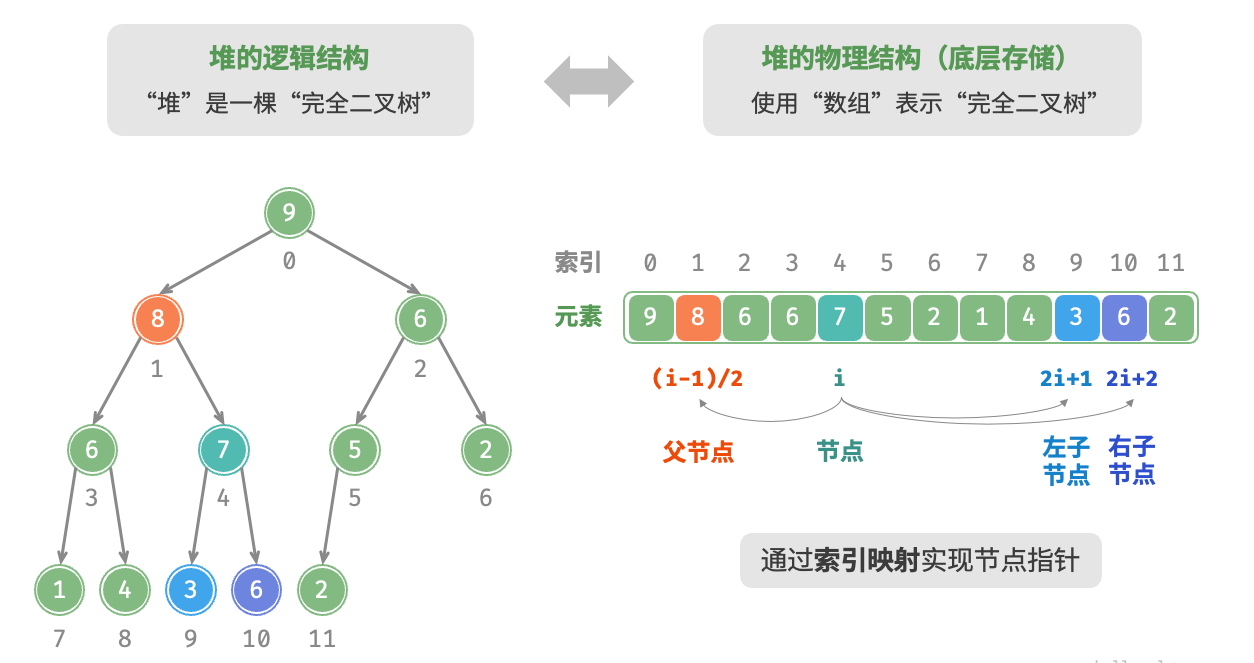
堆是个完全二叉树，因此底层可以用数组来表示。最小堆：

• 插入时，放到最后面，然后与父节点比较对调，直到 >= 父节点；
• 删除时，将最后一个元素放到一个元素（最后置为NULL），与子节点比较对调，直至 <= 子节点；

并查集

假设元素间有关联，且存在传递关系，如何快速判断两个元素是否有关联。

用途

1、维护无向图的连通性。支持判断两个点是否在同一连通块内； 2、判断增加一条边是否会产生环：用在求解最小生成树的Kruskal算法里；

定义：管理一系列不相交的集合，只支持两种操作：

• 合并（Union）：把两个不相交的集合合并为一个集合。
• 查询（Find）：查询两个元素是否在同一个集合中。

初始版本（合并复杂度/查询复杂度：O(h)，h表示树的高度，最差为链表）

算法过程：每个元素只知道自己的父节点；

• 初始每个元素父节点即自身或者 -1，ids[i] = i；

• 查找元素所属的集合

int find(i) {
    while (ids[i] != i) {
        i = ids[i];
    }
    return i;
}

• 合并两个元素时，将其中一个节点的集合指向另一个节点，ids[find(i)]=j；

• 判断两个是否处于同一个集合，find(i)==find(j)；

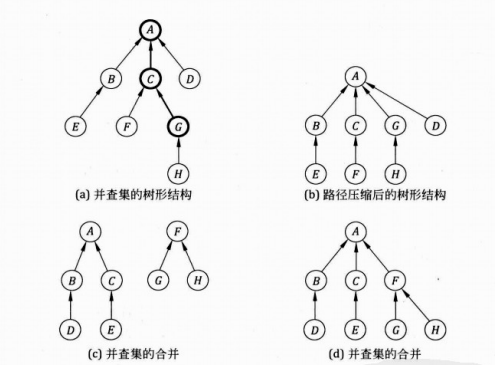
路径压缩

• 解决查找时次数过多的问题，防止树变成链表，查找复杂度变为O(n)；
• 查找时将x到根节点路径上的所有点的parent设为根节点，该优化方法称为压缩路径

按秩合并

• 维护每个子树的节点个数，合并时将小的子树合并到大的子树上
• 如果是维护子树的高度，则路径压缩会造成rank不准确，因此按照 size 进行合并；

树状数组

树状数组（Binary Index Tree, BIT），最简单的树状数组支持两种操作，时间复杂度均为 Olg(n)：

• 单点修改：更改数组中一个元素的值
• 区间查询：查询一个区间内所有元素的和

对于普通数组而言，单点修改的时间复杂度是O(1)，但区间求和的复杂度是O(n)。

原理

树状数组的定义：

• 二进制数最右边的一个1，连带着它之后的0为\(lowbit(x)\)，用\(C(i)\)维护区间\((A_i-lowbit(A_i), Ai]\)，这样查询前n项和时需要合并的区间数是少于\(log_2(n)\)：

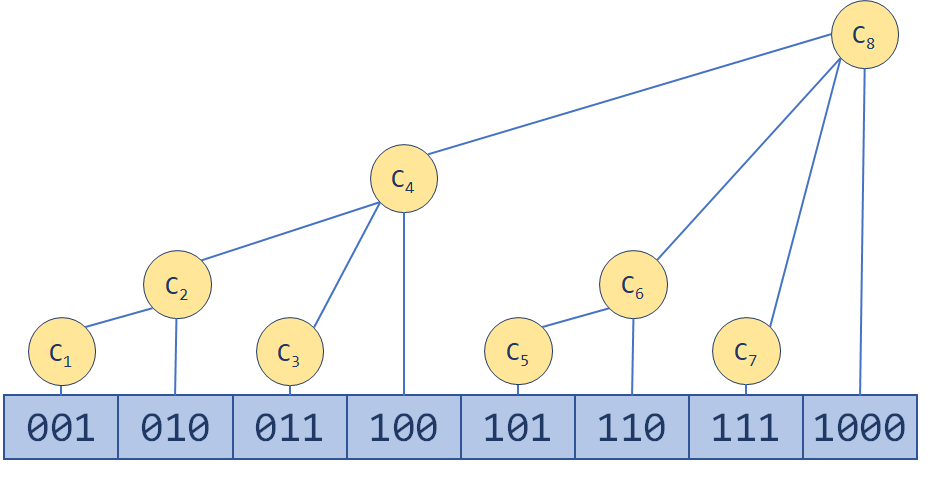
更新就是一个“爬树”的过程。一路往上更新，直到MAXN（树状数组的容量）。

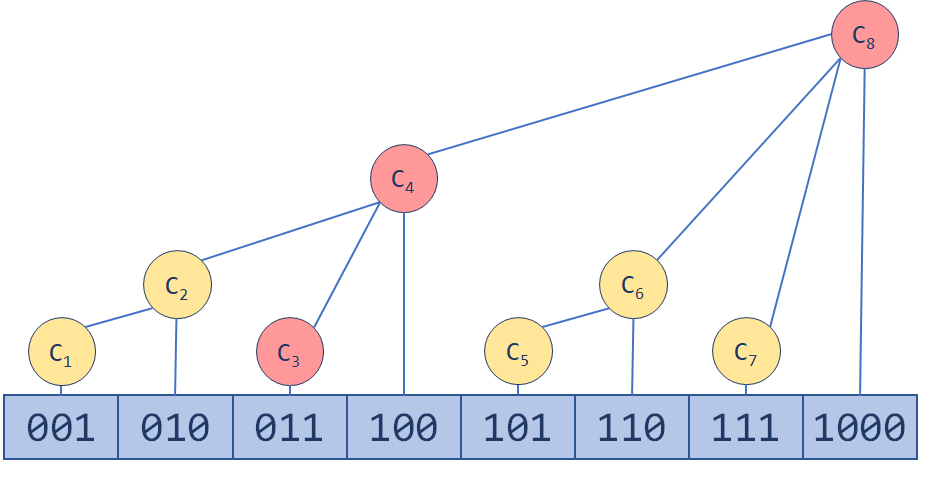
\(lowbit(x)=(x)\&(-x)\)